ROTACIÓN DE EJES

Es una aplicacion de los puntos de un sistema de coordenadas cartesianas ( x , y ) sobre los puntos de un swgundo sistema de coordenadas cartesianas denominado (x' , y') en el que el origen se mantiene fijo. Los ejes X' y Y' se obtiene giradno los ejes (x,y) en sentido contrario.

  

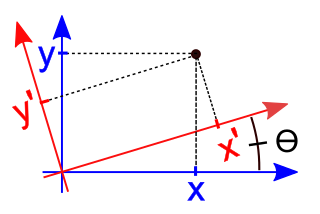
Esto es denominado de la siguiente manera:

* x= x' Cos Ө - y' Sen Ө      * y= y' Cos Ө + x' Sen Ө

SOLUCION

* x'= x Cos Ө + y Sen Ө      * y'= y Cos Ө - x Sen Ө


Para convertir Grados a Radianes y  de Radianes a Grados:

                         π
                  Ө=  -- = 0º
                          8

Grados a Radianes                                          Radianes a Grados

- Sea Ө un angulo                                           - Sea x un radian
        π                                                                   180º
Ө ( ---- )  = radianes                                       x (  ---- ) = Өº
      180º                                                                  π


EJEMPLO 1

Sea x^2-y^2-9=0 una ecuación. Transformar mediante una rotación de 45º de sus originales. Encontrar la nueva ecuacion.
Solucion:

x= [x'Cos 45º] - [y'Sen 45º] = x'√2/2  - y√2/2

y= [x'Cos 45º] y [y'Sen 45º] = x'√2/2  + y√2/2


x= x'√2/2  - y√2/2       y= x'√2/2  + y√2/2

Sustituir x,y en ecuacion original.
(√2x'/2  - y√2y'/2)^2 - (√2x'/2  + √2y'/2)^2 - 9 = 0

[(√2x'/2)^2 -2 (√2x'/2)  -(√2y'/2)^2 +  (-√2y'/2)^2)] - [(√2y'/2)^2) + 2 (√2x'/2) (√2y'/2) + (√2y'/2)^2-9= 0

(x'/2^2 - x'y' + y'/2) - (x'/2 +x'y'+y'^2/2)-9=0

x'/2^2 - x'y' + y'/2 - x'/2 +x'y'+y'^2/2-9=0

-2x'y'-9= 0

2x'y'+9=0

y'= -9/2x'

                       x' 丨y'= -9/2x'
                    -2      2.25
                    -1      4.5
                     0       0
                     1      -4.5
                     2      -2.25
                     3      -1.5
                     4      -1.125

Para concluir se grafica pero en las nuevas coordenadas.


EJEMPLO 2

Transformar la ecuacion 2x'^2+√3xy+y^2=4 girando los ejes a un angulo π/6

SOLUCION:
Transformar π/6 a grados = 30º

x= (x'Cos30º-y'Sen30º) = x'√3/2 - y'/2

y= (x'Cos30º+y'Sen30º) = x'/2 + y'√3/2

Sustituimos X y Y en la ecuacion.

2(√3x'/2-y'^2/2)^2 + √3(x'√3/2-y'/2) (x'/2+y'√3/2)+(x'/2+√3y'/2)^2= 4

2[(√3x'/2)^2+2(√3/2x')(-y'/2)+(-y'/2)^2]+√3(√3x'^2/4+
3x'y'/4-x'y'/4-√3+y'^2+[(x'/2)+2(x'/2)(√3y'^2/2+(√3y'/2)^2]=4

2(3x'^2/4-√3x'y'/2+y'^2)+3x'^2/4+3√3x'y'/4-3√3x'y'-√3x'y'/4-3x'^2/4+x'^2/4+3y'^2/4=4

3x'^2/2-√x'y'+y'^2/2+3x'^2/4+3√3x'y'/4-√3x'y'/4-3y'^2/4+y'^2/4+√3x'y'/2+3y'^2/4=2

1/2(5x'^2+4'^2=4

5x'^2+y'^2=8

Se puede realizar una elipse con la anterior ecuación.
Por lo tanto:

5x^2/8+y^2/8=1

x       y
--- + --- = 1
5/8    8

a=2√2             LL'= 2b^2/a = 5√2/16            v(0,√2/2)      v'(0,-2√2)
b=√10/4         VV'=2a= 4√2                          f(0,√118/4)   f'(0,-√118/4
c= 118/4         FF'=2c= √118/2                     A(√10/4,0)    A'(-√10/4,0)
                       AA'= 2b= √1'/2
                       e=  c/a=     √59/8

Por ultimo. Se grafica en las nuevas coordenadas.

A continuacion un breve video, el complemento del video lo podran encontrar en el siguiente Tema.