Es la figura por la cual una relación, expresión o figura se cambia en otro siguiendo una ley dada y tenemos el siguiente teorema.
TEOREMA
Si se trasladan los ejes coordenados a un nuevo origen O' (h,k) y si las coordenadas de cualquier punto "P" antes y después de la traslación (x,y) y la coordenada (x',y') respectivamente las ecuaciones de transformación del sistema primitivo al nuevo sistema de coordenadas son las siguientes: 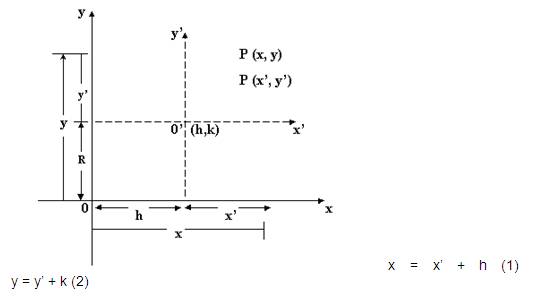

Donde P(x' + h , y' + k)
EJEMPLO 1
Transformar la ecuación: x^3-3x^2-y^2+3x+4y-5=0.
Trasladando los ejes en el nuevo origen (1,2) O'(h,k)
Sabemos que:
x= x' + h y= y' + k
Sustituir X y Y en la ecuación.
(y'+1)^3-3(x'+1)^2-(y'+2)^2+3(x'+1)+4(y'+2)-5=0
x'^3 + 3x'^2 + 3x' + 1-3x'^2 - 6x'-3-y'^2-4y'-4+3x'+3+4y'+8-5=0
x'^3-y'^2=0
y'=√x'^3 x│y= √x'^3
2 2.8
3 5.1
4 8
5 11.1
Por ultimo paso, graficar la siguiente funcion.
EJEMPLO 2
Para una traslacion de los ejes coordenados transformar la ecuacion x^2-4y^2+6x+8y+1=0
x= x' + h y= y' + k
(x'+h)^2-4(y'+k)^2+6(x'+h)+8(y'+k)+1=0
x^2+2(x')(h)+h^2-4(y'^2+2(y')(k)+k^2+6x'+6h+8y'+8k=0
x'^2+2x'+h+h^2-4y'^2+2y'k+k^2+6x'+6h+8y'+8k+1=0
x'(-2h+6)-y'(8k-8)+x'^2+h^2-4y'^2-4k^2+6h+8y'+8k+1=0
Despejar "h" y "k"
2h+6=0 8k-8=0
2h=-6 8k=8
h=-6/2 k=8/8
h= -3 k= 1
O' ( -3 , 1 )
Sustituir h y k en la ecuacion
x'(2(-3)+6)-y'(8-8)+x'^2+(-3)^2-4y'^2-4+6(-3)+8+1=0
x'^2-4y'^2-4=0
x'^2-4y'^2=4
x`^2 y'^2
------- - -------- = 1
4 1
Se concluye resolviendo la siguiente hipérbola.
EJEMPLO 3
Encuentra las nuevas coordenadas del punto (4, -2) si el origen se mueve a (-2 , 3)
Solucion
x= x' + h x' = x-h
y= y'+k ⇒ y' =y-k
x'= x-h y'= y-k
x'= 4-(-2) y'= -2-3 P ( 6 , -5 )
x' = 6 y = -5


No hay comentarios.:
Publicar un comentario