LA RECTA

Presentador de blog.Dale click a Presentador

Segmento Rectilíneo

Porción de una recta emprendida entre 2 de sus puntos donde "A" y "B" son llamados extremos del segmento. 
Donde "A" es origen y "B" punto final. De acuerdo a la dirección del segmento que se tenga.

AB=BA

-Si tenemos 2 puntos de un segmento A y B existe un punto C que los divide. 

HIPERBOLA

Lugar geométrico de un punto que se mueve en un plano de tal manera que el valor absoluto de la diferencia de sus distancias a 2 puntos fijos del plano, llamados focos es siempre igual a una cantidad constante, positiva y menor que la distancia entre los puntos.


PARTRES DE LA HIPERBOLA.



TEOREMA.
*ECUACION ORDINARIA DE LA HIPERBOLA

La ecuacion de la hiperbola de centro en el origen, eje focal, coincida con el eje "x" los focos F(0,c) , F'(-c , 0) . V(a.0) V'(-a,0) y A(0,b) A'(0, -b)

 

Si el el eje focal coincide con el eje "y" los focos F(0,c) , F'(0,-c) . V(0,a) V'(0,-a) y A(b,0) A'(-b,0)



a=Longitud del semieje transverso
b= Longitud del semieje conjugado
c= Distancia del centro a cada foco
 Donde

     c^2= a^2 + b^2

LL'= 2b^2/a         Lado Recto
VV'= 2a               Eje transversal
FF'= 2c                Eje focal
AA'= 2b               Eje conjugado

e= c/a

EJEMPLO:

Sean V(0,3) , V'(0,-3) vertices de una hiperbola y tiene como focos f(0,5) , f'(0,-5)

*PARALELO "Y"*

VV'= d = 2a = 6
d = 6
FF'= d = 2c= 10
10 = 2c
c= 5

b=√c^2 - a^2
 b = 4

LL' = 32/3
AA'= 8                          A(4,0) A'(-4,0)
e= 5/3                 

A continuacion un video para tu comodidad.

SIMPLIFICACIÓN DE ECUACIONES POR TRANSFORMACIÓN DE COORDENADAS.

  TEOREMA
Si efectuamos un cambio de ejes coordenados mediante una traslacion y una rotacion, tomados en cualquier orden y las coordenadas de cualquier punto "P" referido a los sistemas originales y final son: (x,y) y (x'',y'') respectivamente por la cual las ecuaciones de transformacion del sistema original al nuevo sistema son:

Para esto se utiliza:

x' = x'' Cos θ -y'' Sen θ         y' = x'' Sen θ+ y'' Cos θ 

Para esto se utilizara:
x' = (x'' Cos θ -y'' Sen θ) + h         y' = (x'' Sen θ+ y'' Cos θ) + k 

EJEMPLO 1

Por transformacion de coordenadas, simplificar la ecuacion 3x^2-2xy+3y^2-2x-10y+9=0.

Sabemos que:

x= x'+h       y = y'+k

Por lo tanto trasladamos para encontrar (h,k)

3(x'+h)^2-2(x'+h)(y'+k)+3(y'+k)^2-2(x'+h)-10(y'+k)+9=0

3(x'^2+2x'h+h?2)-2(x'y'+x'k+hy'+hk)+3(y'^2+2y'k+k^2-2x'-2h-10y'-10k)+9=0

3x'^2+6x'h+3h^2-2x'y'+2x'k+2hy'+2hk+3y'^2+6y'k+3k^2-2x'-2h-10y'-10k+9=0

3x'^2+3h^2-2x'y'+2hk+3y'^2+3k^2-2h-10k+9+x'(6h-2k-2)+y'(-23h+6k-10)=0

Se construye un sistema de ecuaciones para encontrar (h,k)

 6h-2k=2.........1
-2h+6k=10......2

Multiplicamos por un 3  a la ecuación 2 para eliminar h y de esa formar saber el valor de k.
Entonces...

       6h-2k=2
 +  3(-6h+18k=30)
------------------------
       0  + 16k= 32
              k=32/16
            k= 2

Sustituimos k=2 en la ecuación 1 para obtener el valor de h.

           6h-2(2)=2
           6h-4=2
           6h=6
           h= 6/6
           h= 1

                                 Coordenadas (h,k) son = (1 , 2)

Para encontrar la nueva ecuación, sustituir h=1  k=2

3x'^2+3h^2-2x'y'+2(h)(k)+3y`^2+3k^2-2h-10k+9=0

3x'^2+3(1)^2-2x'y'-2(1)(2)+3y`^2+3(2)^2-2(1)-10(2)+9=0

3x`^2+3-2x'y'-4+3y'^2+12-2-20+9=0

3x'^2-2x'y'+3y'^2-2=0 ⇐ Nueva ecuación.

Usando el teorema de rotacion:

x' = x'' Cos θ -y'' Sen θ         y' = x'' Sen θ+ y'' Cos θ 

Sustituir x' , y' en la nueva ecuacion.

3(x''-cosθ-y''senθ)^2-2[(x''Cosθ-y''Senθ)(x''Senθ+y''Cosθ]+3(x''Senθ+y''Cosθ)^2-2=0

3[x''Cosθ)^2+2(x''Cosθ)(-y''Senθ)+(-ySenθ)^2]-2[x''^2SenθCosθ+x''y''Cos^2θ-x''y''Sen^2θ-y''^2SenθCosθ] +3[(x''Senθ)(y''Cosθ)+(y''Cosθ)^2)]-2=0

3x''^2Cos^2θ-6x''y''SenθCosθ+3y''^2Sen^2θ-2x''^2SenθCosθ-2x''y''Cos^2θ+2x''y''Sen^2θ+2y''^2SenθCosθ+3x''^2Sen^2θ+6x''^2SenθCosθ+3y''Cos^2θ-2=0

3x''^2Cos^2θ-2x''^2SenθCosθ+3x''^2Sen^2θ+3y''^2Sen^2θ+2y''^2SenθCosθ+3y''Cos^2θ+x''y''[-6SenθCosθ-2Cos^2θ+2Sen^2θ+6SenθCosθ]-2=0

3x''^2[Cos^2θ+Sen^2θ]-2x''^2SenθCosθ+3y''^[2Sen^2θCos^2θ+2y''^2]+2y''^2SenθCosθ+x''y''[-SenθCosθ-2Cos^2θ+2Sen^2θ+6SenθCosθ]-2=0

3x''^2-2x''^2SenθCosθ+3y''^2+2y''^2SenθCosθ+X''y''[-2Cos^2θ+2Sen^2θ]-2=0

-2Cos^2θ+2Sen^2θ=0
  2Sen^2θ=2Cos^2θ

Sen^2θ=Cos^2θ(1)

Sen^2θ
--------- = 1
Cos^2θ

Tan^2θ=1

Tanθ=√1

SUSTITUIMOS
3x''^2-2x''^2Sen(45º)+3y''^2Sen(45º)+3y''^2Sen(45º)Cos(45º)=2

3x'^2-2x''^2(√2/2)(√2/2)+3y''^2+2y''^2(1/2)=2

3x''^2-x''^2+3y''^2+y''^2=2

2x''^2+4y''^2=2

x''^2        y''^2

------ +  ----- = 1   (Elipse)

   1           2

b^2=1
a^2=2
c=1

Concluimos con una gráfica.

A continuación unos vídeos para una mayor retroalimentacion, continuación del tema anterior.

ECUACIÓN SIMÉTRICA DE LA RECTA

La recta cuyas intersecciones son los ejes X y Y son "A" distinto de 0 (cero), A distinto de 0 y B distinto de 0 respectivamente, tienen por ecuacion la siguiente.

                                           X               Y
                                       -------    +    ------ = 1
                                            a                b

COROLARIO.
La condicion necesaria y suficiente para que 2 rectss sean perpendiculares entre si, es que el producto de sus pendientes sea -1.


- EJEMPLO 1 :

Hallar la ecuacion de la recta que pasa por el punto (-3 , 1) y es paralela a la recta determinada por los 2 puntos (0 , -2) y ( 5,2).

  y - y1= m (x - x1)


        y2 - y1         2 - (-2)        2 + 2         4
m= ----------- =  ----------- =  --------- =  ----
        x2 - x1          5 - 0              5            5


                 5
   y - 1 =  ---- (x + 3)
                 4

5y - 5 = 4x + 12

4x + 12 - 5y + 5 = 0

4x - 5y + 17 = 0


- EJEMPLO 2 :
Halla la ecuacion de la mediatriz del segmento (-2 , 1) y (3 , -5)

      x1 + x2                                                y1 + y2
x= -----------                                        y = ----------
           2                                                           2


       -2 + 3         1                                        1 - 5        -4
x=  --------- =  ----                                y=  ------- =   ----
           2             2                                           2            2

      -5 -1         6
m= ------- =  - ---
       3 + 2        5

               5            1
 y + 2 = ---- (x -  --- )
               6            2

y + 2 = 5x - 5
             -------
                12


12y + 24 = 5x - 5

5x - 5 - 12y - 24 = 0


5x - 12y -29 = 0

A continuacion estos videos muestran como pasar la ecuacion general a simetrica

GEOMETRÍA ANALÍTICA DEL ESPACIO.

SISTEMA DE COORDENADAS RECTANGULARES EN EL ESPACIO.
Un punto "p" en el espacio tiene una y solamente una coordenada (x,y,z) relativa a un sistema coordenado rectangular especifico.




Ejemplo
Ubica los puntos.

P(-3,-5,3)
Q(3,4,-2)

Distancia entre 2 puntos en el espacio.

Teorema:Sea D la diustancia entre 2 puntos P(x1,y1,z1) y Q (x2,y2,z2) la distancia esta dada por la siguiente formula:


                                            d= √(x2-x1)^2+(y2-y1)^2+(z2-z1)^2

Division de un segmento.
Teorema:
Si P(x1,y1,z1) y Q(x2,y2,z2) son los extremos de 1 segmento, las coordenadas (x,y,z) le pertenecen a un punto "s" el cual divide al segmento PQ.

CONOCEMOS LA RAZON PERO NO CONOZCO EL PUNTO S(X,Y,Z)

X= X1+rX2          Y= Y1 + rY2            Z= Z1 + rZ2
     -----------                ------------                 ------------
        1 + R                       1 + r                          1 + r

CONOCEMOS S(X,Y,Z) PERO NO A "r"

r= X - X1              r= Y - Y1          r= Z - Z1

    ----------                 ---------              ----------

     X2 - X                   Y2 - Y                Z1 - Z

NOS DICE QUE S(X,Y,Z) ES PUNTO MEDIO, ENTONCES r = 1X= X1 + X2         Y = Y1 + Y2         Z= Z1 + Z2

     ------------              ------------             -----------
            2                             2                           2

EJEMPLO 1
Ubica los puntos en el espacio.

A(2,0,-1) B(4,-3,7) c(-5,-9,2) D(3,-2-4) E(0,-3,-9) F(-7,5,-6)

EJEMPLO 2

Traza el siguiente triangulo con coordenadas A(2,-1,3) B(-1,1,2) C(1,5,-2)

d1= √(-1-2)^2+(1--1)+(2-3)^2 = 8
d2= √(1--1)^2+(5-1)^2+(-2-2)^2 = 34
d3= √(2-1)^2+(-1-5)^2+(3-2)^2= 62

x=  1+ (-3)   2                     y = 5+ (-3) (-1)               z= -2+(-3)(3)
   ------- = 2.5                    -------------- = -1              ------------- = -5.5

        1+ (-3)                                   1+(-3)                          1 + (-3)

PUNTO (2.5,-1,-5.5)

COORDENADAS POLARES.

En el sistema polar, un punto se localiza especificando su posición relativa con respecto a una recta fija y a un punto fijo de esa recta. La recta fija se llama eje polar, el punto fijo se llama "polo". El punto "p" es ubicado si solo si se conoce cA θ donde son conocidas como coordenadas polares de "P" primero se escribe el radio, vector y luego el angulo.


Donde: x= rCosθ  y= rSenθ

Donde OA= Eje polar
O= Polo
P= Punto Cualquiera
r= Longitud o radio vector
AOP = Forma del angulo
θ = Angulo polar, angulo vectorial o argumento de P

Para ello hacemos uso de lo siguiente:

Esto es importante, ya que debemos saber la ubicación de los ángulos.

EJEMPLO 1
Ubica los siguientes puntos en el eje polar.

P(4,π/6)                        Nota: El inverso de un angulo, lo calculamos como:
Q(6,2)                              θ= θ+π      ፀ= ፀ+180º
R(-7,75º)
S(5, 7π/4)

Transformar de coordenadas polares a rectangulares y viceversa.

TEOREMA
Si el polo y el eje polar del sistema de coordenadas polares coinciden respectivamente con el origen y la parte positiva del eje "x" de un sistema de coordenadas rectangulares, el paso de una de otra de estos 2 sistemas puede efectuarse por modo de las siguientes formulas.

x= r Cos ፀ                         r^2= x^2 + y^2           r= +-√x^2 + y^2                  Cos θ=+- x/ √ x^2 + y^2
y= r Senፀ                          ፀ= tan -1 y/x              Sen ፀ = +- y/ √x^2 + y^2


EJEMPLO 2
Hallar las coordenadas rectangulares de P, cuyas coordenadas polares son ( 4 , 120º )

Datos           Formula            Sustitucion                    Operacion          Resultado
r = 4             x= r Cos θ          x= 4 Cos (120º)            x= -2                     p(-2, 2√3)
θ = 120        y= r Sen θ           y= 4 Sen (120º)            y= 2√3


EJEMPLO 3 

Hallar la ecuacion polar del lugar geometrico cuya ecuacion es:

                                                        x^2 + y^2 - 4x - 2y + 1= 0
Solucion r^2
Sabemos que:                                 r^2= x^2 + y^2
                                                       x= r Cos θ 
                                                       y= r Sen θ

Sustituimos la ecuacion Original:

                                                    r^2- 4(rCosθ)-2(Senθ)+1= 0

EJEMPLO 4
Transformar la ecuacion rectangular a polar.
                                     
                                                 2x^3+2y^2+2x-6y+3=0

Sabemos que:
                                                       r^2= x^2 + y^2
                                                       x= r Cos θ 
                                                       y= r Sen θ


                         2(rCosθ)^3+2(rSenθ)^2+2(rCosθ)-6(rCosθ)+3=0

Ejemplo 5
Transformar la ecuacion de rectangular a polar.

                                                       x^2 - y^2 = 9

(rCosθ)^2-(rSenθ)^2= 9
r^2(Cosθ)^2-r^2(Sen θ)^2= 9
r(Cosθ)^2 - r(Senθ)^2= 9
r(Cosθ)^2-(Senθ)^2= 9
                                                              9
                                       r= ------------------------------
                                                (Cosθ)^2 - (Senθ)^2



A continuación un vídeo, el cual explica de manera mas especifica los pasos en los ejemplos leídos anteriormente. 

DISTANCIA ENTRE 2 PUNTOS DE COORDENADAS POLARES.

Sean P la coordenada (r1,θ1) y Q(r2, θ2) 2 puntos cuales quieran en un eje polar, su distancia esta dada por la siguiente formula

                                          d=√r1^2+r2^2-2(r1)(r2)Cos( θ1-θ2)

Ejemplo 1
Demostrar que las coordenadas siguientes son vertices de un triangulo.

A(3,π/6) = (3,30º)
B(7,π/3) = (7,60º)
C(3,π/2) = (3,90º)

d = AB = √9+49-2(3)(7)*Cos(30º-60º) = 4.65
d = BC = √49+9-2(7)(3)*Cos(60º-30º) = 4.65
d = CA = √9+9-2(3)(3)*Cos(90º-30º) = 3


EJEMPLO 2
A(0,90º)
 B(1,60º)
C(2,45º)
D(3,0º)

d = AB = √0+1-2(0)(1)*Cos(90º-60º)= 1
d = BC = √1+4-2(1)(2)*Cos(60º-45º)= 1.06
d = CD = √4+9-2(2)(3)*Cos(45º-0º)= 2.12
d = CA = √9+0-2(3)(0)*Cos(0º-90º) = 3






Ejemplo 3
A(1,60º)
B(√6,30º)
C(1,0º)

d = AB  = √1+3-2(1)(√3)*Cos(60º-30º) = 1
d = BC = √3+1-2(√3)(1)*Cos(30º-0º) = 1
d = CA = √1+1-2(1)(1)*Cos(0º-60º) = 1


A continuacion, los siguientes videos te podran brindar mayor proporcion de conocimientos sobre este tema.

ROTACIÓN DE EJES

Es una aplicacion de los puntos de un sistema de coordenadas cartesianas ( x , y ) sobre los puntos de un swgundo sistema de coordenadas cartesianas denominado (x' , y') en el que el origen se mantiene fijo. Los ejes X' y Y' se obtiene giradno los ejes (x,y) en sentido contrario.

  

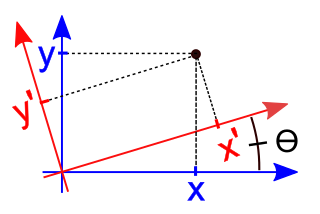
Esto es denominado de la siguiente manera:

* x= x' Cos Ө - y' Sen Ө      * y= y' Cos Ө + x' Sen Ө

SOLUCION

* x'= x Cos Ө + y Sen Ө      * y'= y Cos Ө - x Sen Ө


Para convertir Grados a Radianes y  de Radianes a Grados:

                         π
                  Ө=  -- = 0º
                          8

Grados a Radianes                                          Radianes a Grados

- Sea Ө un angulo                                           - Sea x un radian
        π                                                                   180º
Ө ( ---- )  = radianes                                       x (  ---- ) = Өº
      180º                                                                  π


EJEMPLO 1

Sea x^2-y^2-9=0 una ecuación. Transformar mediante una rotación de 45º de sus originales. Encontrar la nueva ecuacion.
Solucion:

x= [x'Cos 45º] - [y'Sen 45º] = x'√2/2  - y√2/2

y= [x'Cos 45º] y [y'Sen 45º] = x'√2/2  + y√2/2


x= x'√2/2  - y√2/2       y= x'√2/2  + y√2/2

Sustituir x,y en ecuacion original.
(√2x'/2  - y√2y'/2)^2 - (√2x'/2  + √2y'/2)^2 - 9 = 0

[(√2x'/2)^2 -2 (√2x'/2)  -(√2y'/2)^2 +  (-√2y'/2)^2)] - [(√2y'/2)^2) + 2 (√2x'/2) (√2y'/2) + (√2y'/2)^2-9= 0

(x'/2^2 - x'y' + y'/2) - (x'/2 +x'y'+y'^2/2)-9=0

x'/2^2 - x'y' + y'/2 - x'/2 +x'y'+y'^2/2-9=0

-2x'y'-9= 0

2x'y'+9=0

y'= -9/2x'

                       x' 丨y'= -9/2x'
                    -2      2.25
                    -1      4.5
                     0       0
                     1      -4.5
                     2      -2.25
                     3      -1.5
                     4      -1.125

Para concluir se grafica pero en las nuevas coordenadas.


EJEMPLO 2

Transformar la ecuacion 2x'^2+√3xy+y^2=4 girando los ejes a un angulo π/6

SOLUCION:
Transformar π/6 a grados = 30º

x= (x'Cos30º-y'Sen30º) = x'√3/2 - y'/2

y= (x'Cos30º+y'Sen30º) = x'/2 + y'√3/2

Sustituimos X y Y en la ecuacion.

2(√3x'/2-y'^2/2)^2 + √3(x'√3/2-y'/2) (x'/2+y'√3/2)+(x'/2+√3y'/2)^2= 4

2[(√3x'/2)^2+2(√3/2x')(-y'/2)+(-y'/2)^2]+√3(√3x'^2/4+
3x'y'/4-x'y'/4-√3+y'^2+[(x'/2)+2(x'/2)(√3y'^2/2+(√3y'/2)^2]=4

2(3x'^2/4-√3x'y'/2+y'^2)+3x'^2/4+3√3x'y'/4-3√3x'y'-√3x'y'/4-3x'^2/4+x'^2/4+3y'^2/4=4

3x'^2/2-√x'y'+y'^2/2+3x'^2/4+3√3x'y'/4-√3x'y'/4-3y'^2/4+y'^2/4+√3x'y'/2+3y'^2/4=2

1/2(5x'^2+4'^2=4

5x'^2+y'^2=8

Se puede realizar una elipse con la anterior ecuación.
Por lo tanto:

5x^2/8+y^2/8=1

x       y
--- + --- = 1
5/8    8

a=2√2             LL'= 2b^2/a = 5√2/16            v(0,√2/2)      v'(0,-2√2)
b=√10/4         VV'=2a= 4√2                          f(0,√118/4)   f'(0,-√118/4
c= 118/4         FF'=2c= √118/2                     A(√10/4,0)    A'(-√10/4,0)
                       AA'= 2b= √1'/2
                       e=  c/a=     √59/8

Por ultimo. Se grafica en las nuevas coordenadas.

A continuacion un breve video, el complemento del video lo podran encontrar en el siguiente Tema.

TRASLACIÓN DE EJES COORDENADOS

Es la figura por la cual una relación, expresión o figura se cambia en otro siguiendo una ley dada y tenemos el siguiente teorema.

TEOREMA

Si se trasladan los ejes coordenados a un nuevo origen O' (h,k) y si las coordenadas de cualquier punto "P" antes y después de la traslación (x,y) y la coordenada (x',y') respectivamente las ecuaciones de transformación del sistema primitivo al nuevo sistema de coordenadas son las siguientes: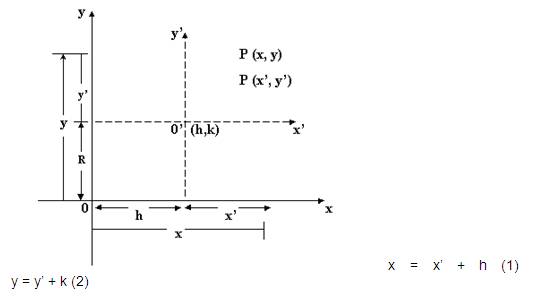                                                           

Donde P(x' + h , y' + k)

EJEMPLO 1

Transformar la ecuación:  x^3-3x^2-y^2+3x+4y-5=0.

Trasladando los ejes en el nuevo origen (1,2) O'(h,k)

Sabemos que:

x= x' + h    y= y' + k

Sustituir X y Y en la ecuación.

(y'+1)^3-3(x'+1)^2-(y'+2)^2+3(x'+1)+4(y'+2)-5=0

x'^3 + 3x'^2 + 3x' + 1-3x'^2 - 6x'-3-y'^2-4y'-4+3x'+3+4y'+8-5=0

x'^3-y'^2=0

y'=√x'^3                 x│y= √x'^3

                              1    1
                              2    2.8
                              3    5.1
                              4    8
                              5    11.1

Por ultimo paso, graficar la siguiente funcion.


EJEMPLO 2
Para una traslacion de los ejes coordenados transformar la ecuacion x^2-4y^2+6x+8y+1=0

x= x' + h    y= y' + k

(x'+h)^2-4(y'+k)^2+6(x'+h)+8(y'+k)+1=0

x^2+2(x')(h)+h^2-4(y'^2+2(y')(k)+k^2+6x'+6h+8y'+8k=0

x'^2+2x'+h+h^2-4y'^2+2y'k+k^2+6x'+6h+8y'+8k+1=0

x'(-2h+6)-y'(8k-8)+x'^2+h^2-4y'^2-4k^2+6h+8y'+8k+1=0

Despejar "h" y "k"

2h+6=0          8k-8=0
2h=-6             8k=8
h=-6/2            k=8/8

 h= -3             k= 1

O' ( -3 , 1 )

Sustituir h y k en la ecuacion
x'(2(-3)+6)-y'(8-8)+x'^2+(-3)^2-4y'^2-4+6(-3)+8+1=0

x'^2-4y'^2-4=0

x'^2-4y'^2=4

  x`^2            y'^2
-------    -    -------- = 1
    4                 1

Se concluye resolviendo la siguiente hipérbola.

EJEMPLO 3
Encuentra las nuevas coordenadas del punto (4, -2) si el origen se mueve a (-2 , 3)

Solucion
x= x' + h        x' = x-h
y= y'+k    ⇒  y' =y-k


x'= x-h                y'= y-k
x'= 4-(-2)            y'= -2-3         P ( 6 , -5 )
 x' = 6                 y = -5

A continuacion se vera de una gran explicacion con los siguientes videos.

Ecuacion de la elipse con centro (H , K)

Paralela  al eje "x" su ecuacion esta dada por:

     ( x - h ) ^2      (y - k ) ^2
    -----------     +  ------------- = 1             F ( h + c , k)
          a^2                 b^2                          F' ( h - c , k)

-Si el eje focal coincide con el eje "y" su ecuacion es :

                              ( x - h )^2        ( y - k )^2
                            -------------    +  ------------- = 1            F(h , k + c)
                                    b^2                  a^2                        F'(h , k - c)

Ejemplo:
Sean V(-3, 7) , V'( -3 , -1) y LL'= 2
Hallar ecuacion.

VV' = 2a = 8                     2a= 8             2b^2/ 4 = 2                         c√16 - 4 = 2√3
AA'= 2b = 4                        a= 4                b^2= 8/2= 4                          c= 2√3
FF'=                                                             b= 2
e=
                             F( -3, 3+2√3)                                   
                             F'(-3, 3-2√3)  absisa = -3

      C(-3,3)
                                      ( x + 3)^2        (y-3)^2
                                  ----------------   +   ------------ = 1
                                            4                        16

ELIPSE

Se mueve en su punto plano, de tal manera que la suma de sus distancias a 2 puntos fijos de ese plano es siempre igual a una constante mayor que la distancia entre los 2 puntos.

Partes de la Elipse.




TEOREMA.
Cuando tenemos centro en el origen ( 0 , 0 )

La ecuación de una elipse de centro en el origen, eje focal, al eje "x", distancia focal igual a 2C y cantidad constante igual a 2.

Su ecuacion:

                                   X^2            Y^2
                               ----------  +  ---------- = 1
                                     a^2             b^2


Si el eje focal de la elipse coincide con el el "y"
La ecuacion es:

                        x^2       y^2
                    --------  + ------ = 1
                         b^2        a^2


"a" Longitud del semieje mayor
"b" Longitud del semieje menor
"a , b y c" estan ligados por la relacion

          a^2 = b^2 + c^2


-Longitud del lado recto


              LL' =    2b
                         -----
                            a


-Excentricidad "e"

                      c
            e =  ------
                      a

-Longitud del eje mayor
             
VV ' = 2A


-Longitud del eje menor

AA ' = 2b

Las coordenadas de los vertices  V y V' estan dadas por

"X" :

(a , 0) y (-a , 0)

"Y"

(0 , a) y ( 0 , -a)


-EJEMPLO: 
Una elipse tiene centro en el origen C(0,0) y su eje mayor coincide con el eje "y".
Uno de sus focos es (0,3) y tiene excentricidad igual a 1/2. Hallar las coordenadas del otro foco, la longitud del eje mayor, del eje menor, la ecuación de la elipse y la longitud del lado recto.

F(0,3)                                                                a^2 = b^2 + c^2
e = 1/2                                                             b^2= a^2 - c^2
FF' = (0,-3)                                                      b = √ 36 - 9
VV'= 2a= 12                                                   
AA'= 2b= 6√13                                               b= 3√3


  x^2       y^2              x^2       y^2
 ------  + ----- = 1 =  ------  +  ----- = 1
    b^2      a^2               27        36


LL' = 2b^2         2 (27)
          ------ =    --------- = 9
             a                6

                 C        3
1/2 = c =  --- =  ----                 a= 6                 c      a

Videos con mayores datos.