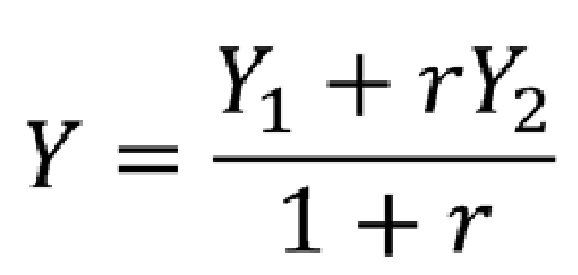Paralela al eje "x" su ecuacion esta dada por:
( x - h ) ^2 (y - k ) ^2
----------- + ------------- = 1 F ( h + c , k)
a^2 b^2 F' ( h - c , k)
-Si el eje focal coincide con el eje "y" su ecuacion es :
( x - h )^2 ( y - k )^2
------------- + ------------- = 1 F(h , k + c)
b^2 a^2 F'(h , k - c)
Ejemplo:
Sean V(-3, 7) , V'( -3 , -1) y LL'= 2
Hallar ecuacion.
VV' = 2a = 8 2a= 8 2b^2/ 4 = 2 c√16 - 4 = 2√3
AA'= 2b = 4 a= 4 b^2= 8/2= 4 c= 2√3
FF'= b= 2
e=
F( -3, 3+2√3)
F'(-3, 3-2√3) absisa = -3
C(-3,3)
( x + 3)^2 (y-3)^2
---------------- + ------------ = 1
4 16
miércoles, 18 de septiembre de 2019
ELIPSE
Se mueve en su punto plano, de tal manera que la suma de sus distancias a 2 puntos fijos de ese plano es siempre igual a una constante mayor que la distancia entre los 2 puntos.
Partes de la Elipse.

TEOREMA.
Cuando tenemos centro en el origen ( 0 , 0 )
La ecuación de una elipse de centro en el origen, eje focal, al eje "x", distancia focal igual a 2C y cantidad constante igual a 2.
Su ecuacion:
X^2 Y^2
---------- + ---------- = 1
a^2 b^2
Si el eje focal de la elipse coincide con el el "y"
La ecuacion es:
x^2 y^2
-------- + ------ = 1
b^2 a^2
"a" Longitud del semieje mayor
"b" Longitud del semieje menor
"a , b y c" estan ligados por la relacion
a^2 = b^2 + c^2
-Longitud del lado recto
LL' = 2b
-----
a
-Excentricidad "e"
c
e = ------
a
-Longitud del eje mayor
VV ' = 2A
-Longitud del eje menor
AA ' = 2b
Las coordenadas de los vertices V y V' estan dadas por
"X" :
(a , 0) y (-a , 0)
"Y"
(0 , a) y ( 0 , -a)
-EJEMPLO:
Una elipse tiene centro en el origen C(0,0) y su eje mayor coincide con el eje "y".
Uno de sus focos es (0,3) y tiene excentricidad igual a 1/2. Hallar las coordenadas del otro foco, la longitud del eje mayor, del eje menor, la ecuación de la elipse y la longitud del lado recto.
F(0,3) a^2 = b^2 + c^2
e = 1/2 b^2= a^2 - c^2
FF' = (0,-3) b = √ 36 - 9
VV'= 2a= 12
AA'= 2b= 6√13 b= 3√3
x^2 y^2 x^2 y^2
------ + ----- = 1 = ------ + ----- = 1
b^2 a^2 27 36
LL' = 2b^2 2 (27)
------ = --------- = 9
a 6
C 3
1/2 = c = --- = ---- a= 6 c a
Videos con mayores datos.
Partes de la Elipse.

TEOREMA.
Cuando tenemos centro en el origen ( 0 , 0 )
La ecuación de una elipse de centro en el origen, eje focal, al eje "x", distancia focal igual a 2C y cantidad constante igual a 2.
Su ecuacion:
X^2 Y^2
---------- + ---------- = 1
a^2 b^2
Si el eje focal de la elipse coincide con el el "y"
La ecuacion es:
x^2 y^2
-------- + ------ = 1
b^2 a^2
"a" Longitud del semieje mayor
"b" Longitud del semieje menor
"a , b y c" estan ligados por la relacion
a^2 = b^2 + c^2
-Longitud del lado recto
LL' = 2b
-----
a
-Excentricidad "e"
c
e = ------
a
-Longitud del eje mayor
VV ' = 2A
-Longitud del eje menor
AA ' = 2b
Las coordenadas de los vertices V y V' estan dadas por
"X" :
(a , 0) y (-a , 0)
"Y"
(0 , a) y ( 0 , -a)
-EJEMPLO:
Una elipse tiene centro en el origen C(0,0) y su eje mayor coincide con el eje "y".
Uno de sus focos es (0,3) y tiene excentricidad igual a 1/2. Hallar las coordenadas del otro foco, la longitud del eje mayor, del eje menor, la ecuación de la elipse y la longitud del lado recto.
F(0,3) a^2 = b^2 + c^2
e = 1/2 b^2= a^2 - c^2
FF' = (0,-3) b = √ 36 - 9
VV'= 2a= 12
AA'= 2b= 6√13 b= 3√3
x^2 y^2 x^2 y^2
------ + ----- = 1 = ------ + ----- = 1
b^2 a^2 27 36
LL' = 2b^2 2 (27)
------ = --------- = 9
a 6
C 3
1/2 = c = --- = ---- a= 6 c a
Videos con mayores datos.
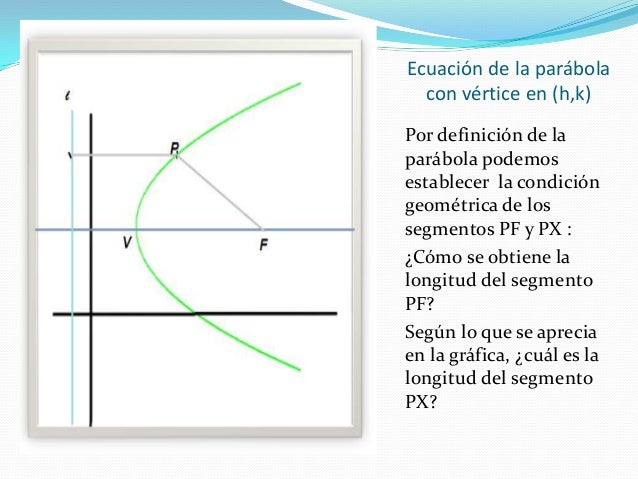
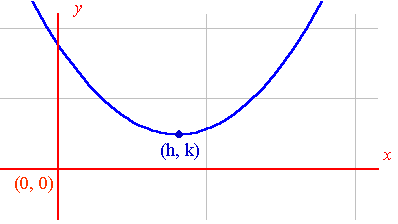
ECUACIÓN DE LA PARÁBOLA CON VÉRTICE (H , K)
Para eje X
( y - k )`2 = 4p (x - h )
Foco = ( x + p , y)
Directriz = x = x - p
P > 0
P < 0
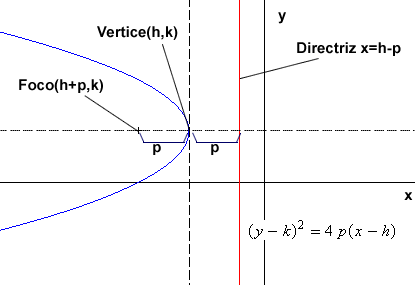
Para eje Y
( x - h )^2 = 4p (y - k )
Foco= (x,y + p)
Directriz = y= y-p
P > 0
FORMULAS GENERALES
Paralelo "x"
y^2 + Dx + Ex + F = 0
Paralelo "y"
x^2 + Dx + Ex + F = 0
EJEMPLO:
Hallar la ecuacion de la parabola cuyo vertice V(3 , 4) F( 3 , 2). Hallar la directriz, longitud del lado recto.
P 丨FV丨= 4 - 2 = 2 P = -2 < 0
( x - h )^2 = 4p (y - k )
( x - h )^2 = -8 (y - k )
Directriz Lado recto :
y = y-p Como 4P = -8 = 8
y= 4 -( -2)
y = 6
Este vídeo contiene información que te ayudara demasiado.
PARABOLA
Lugar geométrico de un punto que se mueve de tal manera que su distancia de una recta fija situada en el plano es siempre igual a su distancia de un punto fijo de un plano que no pertenece a la recta.
PARTES DE LA PARABOLA.


TEOREMA
Para conseguir la directriz cuando el eje coincide en "x"
x= -p
Para conseguir la directriz cuando el eje coincide en "y"
y = -p
*Para ambos casos la longitud del lado recto esta dada por
丨 4P丨

EJEMPLO:
Una parabola cuyo vertice esta en el origen y su eje coincide con el eje y pasa por el punto (4 , -2)
hallar:
-Ecuacion
-Foco
-Directriz
-Lado Recto
x^2= 4py
16 = 4 p (-2)
16 = -8 p
P = -2 P < 0
X^2 = 4 (-2) y ___ Ecuacion
x^2 = -8 y
( 0 , -2)______Foco
y = -2 ______ Directriz
丨 4P丨= 4 (-2) = 8______Lado Recto
PARTES DE LA PARABOLA.

TEOREMA
Para conseguir la directriz cuando el eje coincide en "x"
x= -p
Para conseguir la directriz cuando el eje coincide en "y"
y = -p
*Para ambos casos la longitud del lado recto esta dada por
丨 4P丨

EJEMPLO:
Una parabola cuyo vertice esta en el origen y su eje coincide con el eje y pasa por el punto (4 , -2)
hallar:
-Ecuacion
-Foco
-Directriz
-Lado Recto
x^2= 4py
16 = 4 p (-2)
16 = -8 p
P = -2 P < 0
X^2 = 4 (-2) y ___ Ecuacion
x^2 = -8 y
( 0 , -2)______Foco
y = -2 ______ Directriz
丨 4P丨= 4 (-2) = 8______Lado Recto
ECUACIÓN GENERAL DE LA RECTA
Tiene por ecuación la siguiente:
(x - h)^2 + (y - k)^2 = r^ 2 ⇒ * x^2 + y^2 + Dx + Ex + F = 0 *
EJEMPLO:
Reducir las 3 ecuaciones siguientes a la forma ordinaria de la ecuación de la circunferencia halle su centro y su radio.
A) 2x^2 + 2y^2 - 10x + 6y -15 = 0
B) 36x^2+ 36y^2 + 48x - 108y + 97 = 0
C) X^2 + Y^2 -8x + 6y + 29 = 0
A) 2x^2 + 2y^2 - 10x + 6y -15 = 0
2 * (2x^2 + 2y^2 - 10x + 6y -15) = 0
x2 + y2 - 5x + 3y = 15/2
[ x2 - 5x + (5/2)^2 ] + [ y2 + 3y + (3/2)^2 ] = 15/2 + 25/4 + 9/4 = 16
(x - 5/2)`2 + (y + (3/2)^2 = 16 C( 5/2 , -3/2)
r= 4
A continuación unos cuantos vídeos para su comodidad.
(x - h)^2 + (y - k)^2 = r^ 2 ⇒ * x^2 + y^2 + Dx + Ex + F = 0 *
EJEMPLO:
Reducir las 3 ecuaciones siguientes a la forma ordinaria de la ecuación de la circunferencia halle su centro y su radio.
A) 2x^2 + 2y^2 - 10x + 6y -15 = 0
B) 36x^2+ 36y^2 + 48x - 108y + 97 = 0
C) X^2 + Y^2 -8x + 6y + 29 = 0
A) 2x^2 + 2y^2 - 10x + 6y -15 = 0
2 * (2x^2 + 2y^2 - 10x + 6y -15) = 0
x2 + y2 - 5x + 3y = 15/2
[ x2 - 5x + (5/2)^2 ] + [ y2 + 3y + (3/2)^2 ] = 15/2 + 25/4 + 9/4 = 16
(x - 5/2)`2 + (y + (3/2)^2 = 16 C( 5/2 , -3/2)
r= 4
A continuación unos cuantos vídeos para su comodidad.
ECUACIÓN DE LA CIRCUNFERENCIA.
TEOREMA
La circunferencia cuyo centro es el punto (h , k) y cuyo radio es la constante "r" tiene por ecuacion la siguiente:
* (x - h)^2 + (y - k)^2 *
Corolario.
La circunferencia de centro en el origen y radio "R" tienen por ecuacion a:
* x^2 + y^2 = r^2 *
EJEMPLO:
Hallar la ecuacion de la circunferencia que tiene centro en ( 16/5 , 4/5) y pasa por el punto (1 , -1)
r = 丨CP丨= √ (X1 - X2) + (Y1 - Y2)
= √(16/5 - 1)^2 + ( 4/5 + 1)
=√ 202 / 5 + 202/25
( X - 16/5) ^2 + (Y - 4/5)^2 = 202/25^2
A continuacion una breve explicacion en el video.
martes, 17 de septiembre de 2019
LINEA RECTA, ECUACION Y ECUACION GENERAL
Lugar geometrico de los puntos tales que son diferentes A(X1 , Y1) B(X2 , Y2) y el valor de la pendiente "m" siempre es una constante.
TEOREMA
La recta que pasa por el punto P(X1 , Y1) y tiene pendiente "m", tiene por ecuación la siguiente.
y - y1 = m(x - x1)
- EJEMPLO:
La recta que pasa por el punto (4, -1) tiene pendiente m = -1
y - (-1) = -1 (x - 4)
y +1 = -x +4
y + 1 + x -4 = 0
x + y - 3 = 0
TEOREMA La recta que pasa por 2 puntos dados A(X1 , Y1) , B(X2 , Y2) tiene por ecuacion
y2 - y1
y - y1 = ------------- = (x , x1)
x2 - x1
FORMA GENERAL DE LA ECUACIÓN DE UNA RECTA
-3 -8
----- C - C -----
5 5 -8 -2
B= --------------------- = ------------- = ------ C = B = ------- C
-3 2
( ---- ) X (----- C ) 4 + C = 0
5 5
Diviendo entre C
-3 2
-5(----- X - ---- Y + 1 = 0 )
5 5
Multiplicado por 5
3X + 2Y -5 = 0
El video nos comparte una explicacion mas compleja.
TEOREMA
La recta que pasa por el punto P(X1 , Y1) y tiene pendiente "m", tiene por ecuación la siguiente.
y - y1 = m(x - x1)
- EJEMPLO:
La recta que pasa por el punto (4, -1) tiene pendiente m = -1
y - (-1) = -1 (x - 4)
y +1 = -x +4
y + 1 + x -4 = 0
x + y - 3 = 0
TEOREMA La recta que pasa por 2 puntos dados A(X1 , Y1) , B(X2 , Y2) tiene por ecuacion
y2 - y1
y - y1 = ------------- = (x , x1)
x2 - x1
FORMA GENERAL DE LA ECUACIÓN DE UNA RECTA
La ecuacion de una recta cualquiera en el plano coordenado de la forma lineal.
Ax + By + C = 0
Donde A o B debe ser diferente a cero y C puede o no ser igual a cero.
EJEMPLO:
Hallar los valores que deben tener los coeficientes de la ecuacion general de una recta para que pase por los 2 puntos (-1 , 4) y (3, -2).
Ax + By + C = 0
(-1 , 4)
-A + 4 B + C = 0 ............. 1
(3 , -2)
3A - 2B + C = 0 ................2
Paso 1 Paso 2 Despejar A
-A + 4B + C = 0 - 3
2( 3A - 2B + C = 0) A= ----- C
5
-A + 4B+ C = 0
6A - 4B + 2C= 0
------------------------------
5A + 3C = 0
Paso 3. Sustituimos 1 en A
3
---- C + 4B + C = 0
3
---- C + 4B + C = 0
5
-3 -8
----- C - C -----
5 5 -8 -2
B= --------------------- = ------------- = ------ C = B = ------- C
4 4 20 5
------
1
-3 2
( ---- ) X (----- C ) 4 + C = 0
5 5
Diviendo entre C
-3 2
-5(----- X - ---- Y + 1 = 0 )
5 5
Multiplicado por 5
3X + 2Y -5 = 0
PENDIENTE DE UNA RECTA Y ANGULO FORMADO POR 2 RECTAS
Si A (X1 , Y1) y B ( X2 , Y2) su pendiente se calcula como:
Y2 - Y1
m= --------------
X2 - X1
- EJEMPLO:
A(1 , 6) , B(5, -2) Hallar la pendiente
-2 -6
m = ------------ = -2
5 - 1
TEOREMA:
Sea ፀ un angulo formado por 2 rectas, este se calcula:
m2 - m1
Tan (ፀ) = ---------------
1 + (m1 . m2)
-Existe una gran variedad de ejercicios en este caso, a continuación, estarán disponibles para que puedan acudir a ellos en cualquier momento.
Y2 - Y1
m= --------------
X2 - X1
- EJEMPLO:
A(1 , 6) , B(5, -2) Hallar la pendiente
-2 -6
m = ------------ = -2
5 - 1
TEOREMA:
Sea ፀ un angulo formado por 2 rectas, este se calcula:
m2 - m1
Tan (ፀ) = ---------------
1 + (m1 . m2)
-Existe una gran variedad de ejercicios en este caso, a continuación, estarán disponibles para que puedan acudir a ellos en cualquier momento.
DIVISIÓN DE UN SEGMENTO
Si un punto "A" con coordenadas (X1 , Y2) y BX - X2 Y2. Son los extremos de un segmento y sea C un punto que los divide en una razón dada "R". El valor de sus coordenadas del punto "C" se calculan de la siguiente manera.
A(X1 , Y1) , B(X2 , Y2) , C (X ,Y) que los divide.
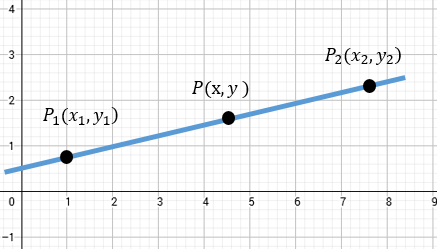
PARA X:
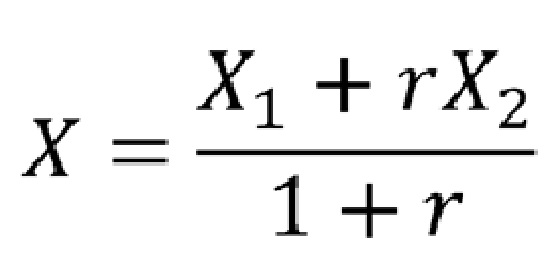
PARA Y:
-EJEMPLO 1:
A(-4,2) B(4,6). Puntos de un extremo y un punto W(X , Y) que divide con una razón de -3. Hallar el punto W
Teniendo las formulas anteriores, para X tenemos que:
-4 (-3) (4) -4 - 12 -16
x= --------------- = ----------- = -------- = 8
1 + (-3) -2 -2
Para Y:
2 + (-3) 6 2 - 18 -16
y= --------------- = ----------- = ---------- = 8
1 + (-3) -2 -2
W = (8 , 8)
- EJEMPLO 2:
Los puntos extremos de 1 segmento son A(2,4) y B(8,4). Hallar el punto C(x , y) que divide a este segmento en 2 partes, tales que su razon es -2.
Teniendo las formulas anteriores, para X tenemos que:
2 + (-2) 8 2 - 16 -14
x= -------------- = ---------- = -------- = 14
1 + (-2) -1 -1
Para Y:
4 + (-2) 4 4 + 8 12
y= -------------- = ---------- = ---------- = -12
1 + (-2) -1 -1
A continuación el siguiente vídeo representa los pasos a seguir de una forma mas compleja.
A(X1 , Y1) , B(X2 , Y2) , C (X ,Y) que los divide.
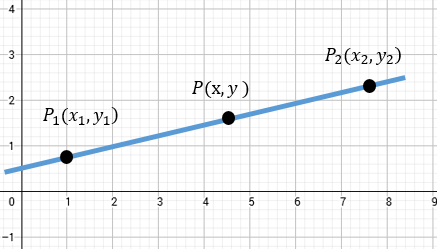
PARA X:
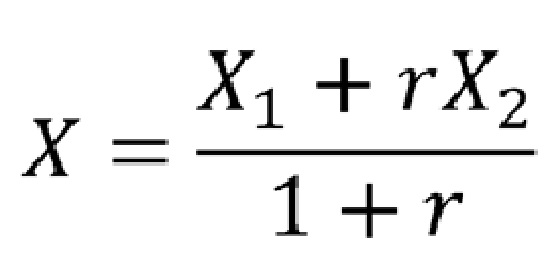
PARA Y:
-EJEMPLO 1:
A(-4,2) B(4,6). Puntos de un extremo y un punto W(X , Y) que divide con una razón de -3. Hallar el punto W
Teniendo las formulas anteriores, para X tenemos que:
-4 (-3) (4) -4 - 12 -16
x= --------------- = ----------- = -------- = 8
1 + (-3) -2 -2
Para Y:
2 + (-3) 6 2 - 18 -16
y= --------------- = ----------- = ---------- = 8
1 + (-3) -2 -2
W = (8 , 8)
- EJEMPLO 2:
Los puntos extremos de 1 segmento son A(2,4) y B(8,4). Hallar el punto C(x , y) que divide a este segmento en 2 partes, tales que su razon es -2.
Teniendo las formulas anteriores, para X tenemos que:
2 + (-2) 8 2 - 16 -14
x= -------------- = ---------- = -------- = 14
1 + (-2) -1 -1
Para Y:
4 + (-2) 4 4 + 8 12
y= -------------- = ---------- = ---------- = -12
1 + (-2) -1 -1
A continuación el siguiente vídeo representa los pasos a seguir de una forma mas compleja.
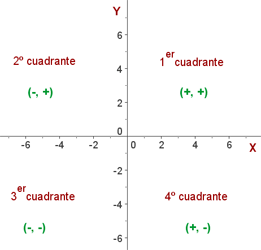
SISTEMA COORDENADO EN EL PLANO
Un sistema coordenado rectangular consta de 2 rectas dirigidas x',x - y',y llamadas coordenadas perpendiculares entre si.
DONDE:
DONDE:
- X'X es llamado eje X o eje de las abscisa.
- Y'Y es llamado eje Y o eje de las coordenadas.
Este sistema coordenado esta dividido en cuatro cuadrantes.
Un punto P en el sistema coordenado esta formado por uno y solamente un par de coordenadas.
P(X1 , Y1)
P(X1 , Y1)
TEOREMA:
La distancia entre 2 puntos P1(X1 , Y1) P2(Y1 , Y2) esta dada por:
La distancia entre 2 puntos P1(X1 , Y1) P2(Y1 , Y2) esta dada por:
EJEMPLO:
Calcular la distancia de los siguientes puntos (-3,-1) , (0,3) , (3,4)
AB d= √ (0-(-3)^2 + (3-(-1)^2 BC d= √(3-0)^2 + (4-3)^2 AC d= √(3-(-3)^2 + (4-(-1)^2
=√9 + 16 = √9 + 1 = √36 + 25
=√25 = √ 10 =√61
= 5 = 3.1 = 7.81
AB d= √ (0-(-3)^2 + (3-(-1)^2 BC d= √(3-0)^2 + (4-3)^2 AC d= √(3-(-3)^2 + (4-(-1)^2
=√9 + 16 = √9 + 1 = √36 + 25
=√25 = √ 10 =√61
= 5 = 3.1 = 7.81
EJEMPLO CON MAYOR DETALLE EN EL VÍDEO
DISTANCIA ENTRE 2 PUNTOS DEL SEGMENTO
Es el valor numérico o valor absoluto del segmento que une a los 2 puntos donde representamos a la distancia por una "D".
X1 X2
d=丨AB丨= 丨BA丨
(X2 - X1) = (X1 - X2)
EJEMPLO:
A(5) , B(-3)
5 -3
d= 丨AB丨= 丨BA丨
(X2 - X1) = (X1 - X2)
-3-5 = 5-(-3)
-8 = 8
8 = 8
Suscribirse a:
Comentarios (Atom)
LA RECTA
Presentador de blog. Dale click a Presentador Segmento Rectilíneo Porción de una recta emprendida entre 2 de sus puntos donde "...

-
SISTEMA DE COORDENADAS RECTANGULARES EN EL ESPACIO. Un punto "p" en el espacio tiene una y solamente una coordenada (x,y,z) relat...
-
Es la figura por la cual una relación, expresión o figura se cambia en otro siguiendo una ley dada y tenemos el siguiente teorema . TEOR...