SISTEMA COORDENADO EN EL PLANO

Un sistema coordenado rectangular consta de 2 rectas dirigidas x',x - y',y llamadas coordenadas perpendiculares entre si.
 
 DONDE:

• X'X es llamado eje X o eje de las abscisa.
• Y'Y es llamado eje Y o eje de las coordenadas.

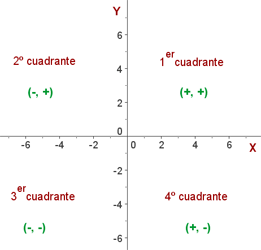
Este sistema coordenado esta dividido en cuatro cuadrantes.

Un punto P en el sistema coordenado esta formado por uno y solamente un par de coordenadas.

                                                                P(X1 , Y1)

TEOREMA: 
La distancia entre 2 puntos P1(X1 , Y1)   P2(Y1 , Y2) esta dada por:
 
                                               
                                                      

EJEMPLO:

Calcular la distancia de los siguientes puntos (-3,-1) , (0,3) , (3,4)

AB d= √ (0-(-3)^2 + (3-(-1)^2            BC d= √(3-0)^2 + (4-3)^2          AC d= √(3-(-3)^2 + (4-(-1)^2
         =√9 + 16                                             = √9 + 1                                      = √36  +  25
         =√25                                                   = √ 10                                          =√61
         = 5                                                      = 3.1                                            = 7.81

EJEMPLO CON MAYOR DETALLE EN EL VÍDEO